
#LINEAR ALGEBRA SYSTEM OF EQUATIONS SOLVER SERIES#
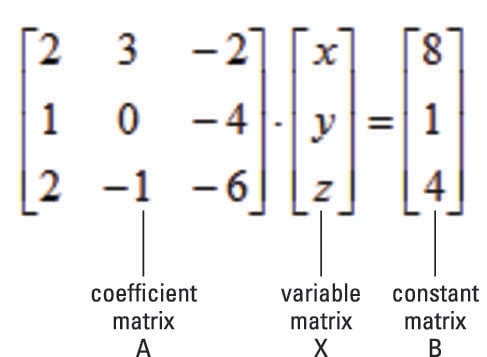
A system is solved by writing a series of systems, one after the other, each equivalent to the previous system. Two such systems are said to be equivalent if they have the same set of solutions. The algebraic method for solving systems of linear equations is described as follows. Is called the constant matrix of the system. Is called the coefficient matrix of the system and The array of coefficients of the variables The augmented matrix is just a different way of describing the system of equations. For clarity, the constants are separated by a vertical line. Each row of the matrix consists of the coefficients of the variables (in order) from the corresponding equation, together with the constant term. Occurring in the system is called the augmented matrix of the system. It is necessary to turn to a more “algebraic” method of solution.īefore describing the method, we introduce a concept that simplifies the computations involved. However, this graphical method has its limitations: When more than three variables are involved, no physical image of the graphs (called hyperplanes) is possible. With three variables, the graph of an equation can be shown to be a plane and so again provides a “picture” of the set of solutions. Then the system has infinitely many solutions-one for each point on the (common) line. The lines are parallel (and distinct) and so do not intersect.Then the system has a unique solution corresponding to that point. The lines intersect at a single point.If the system has two equations, there are three possibilities for the corresponding straight lines: In particular, if the system consists of just one equation, there must be infinitely many solutions because there are infinitely many points on a line. Hence the solutions to a system of linear equations correspond to the points that lie on all the lines in question. Moreover, a point with coordinates and lies on the line if and only if -that is when, is a solution to the equation. When only two variables are involved, the solutions to systems of linear equations can be described geometrically because the graph of a linear equation is a straight line if and are not both zero.

Note that each variable in a linear equation occurs to the first power only. Is a linear equation the coefficients of, , and are, , and, and the constant term is. A finite collection of linear equations in the variables is called a system of linear equations in these variables. Here denote real numbers (called the coefficients of, respectively) and is also a number (called the constant term of the equation). Is called a linear equation in the variables. However, it is often convenient to write the variables as, particularly when more than two variables are involved. Is a straight line (if and are not both zero), so such an equation is called a linear equation in the variables and. If, , and are real numbers, the graph of an equation of the form Linear algebra arose from attempts to find systematic methods for solving these systems, so it is natural to begin this book by studying linear equations. Practical problems in many fields of study-such as biology, business, chemistry, computer science, economics, electronics, engineering, physics and the social sciences-can often be reduced to solving a system of linear equations. 1 System of Linear Equations 1.1 Solutions and elementary operations


 0 kommentar(er)
0 kommentar(er)
